[Paper Review] GEN: Pushing the Limits of Softmax-Based Out-of-Distribution Detection
논문 링크 : GEN
GEN: Pushing the Limits of Softmax-Based Out-of-Distribution Detection (CVPR 2023)논문 리뷰입니다.
Introduction
딥러닝 방법을 실제 상황에서 더 안전하게 사용하려면, 테스트 시 ID Sample인지 아니면 이전에 본 적 없는 OOD Sample인지 구별하는 것이 중요하다. 따라서 deep neural network는 자신이 모르는 것을 인지할 수 있어야 한다.
그러나 Network는 OOD Sample에 대해서도 overconfident하는 예측을 내놓는 경향이 있다. OOD Sample을 탐지하는 다양한 시나리오가 존재하는데 특히 본 논문에서는 Semantic Shift 시나리오에 초점을 맞추어 training set에 존재하지 않는 semantic label을 가진 input을 탐지하는 것을 목표로 한다.
본 논문에서는 Data를 평가하는 scalar score function을 설계하고, ID sample에 더 높은 값을 부여하도록 한다. Classifier의 predictive distribution을 이용하여 score function을 설계한다.
OOD detection을 위한 연구에서 ID data의 feature 정보를 이용하여 성능 향상을 이끌어내는 연구가 있지만, 실용적인 제약이 따른다. 일부 방법은 train data에 접근해야하며 다른 방법들은 feature activation에 접근해야한다. 그러나 상업적으로 배포된 Network들은 일반적으로 blackbox 분류기이며, train data는 기밀 정보일 가능성이 높다.
따라서 본 연구의 목표는 Softmax layer의 output만을 활용하여 OOD detection성능을 극대화한다.

Contribution
- GEN은 predictive distribution만을 사용한다. re-training이나 outlier exposure이 필요없고, 어떤 train data의 통계도 사용하지 않는다.
- 더 제한된 모델 배포 환경에서도 활용가능성이 높다.
- 다른 post-hoc 방법과 비교했을 때, GEN의 score 분포는 ID/OOD를 더 잘 구분한다.
Notation
- $z$ : penultimate layer output
- $f(z)=Wz+b$ : vector of logits
- $W$ : weight matrix
- $b$ : bias vector
- $p=\text{Softmax}(f(z))$ : output of a classifier network
- $\Delta^{C}$ : C차원 unit simplex
Generalized Entropy Score
본 논문의 목표는 OOD detection을 위해 오직 logit 특히 predictive distribution만을 최대한 활용하는 것이다. 이러한 접은 방식은 Classifier training, training set, 명시적인 OOD Sample에 대한 정보에 의존하지 않는다.
논문에서의 주요 가정은 Classifier의 training loss가 순수한 one-hot predictive distribution에서 최소가 되는 항에 지배된다는 것이다. 따라서 training data에 가까운 ID test sample은 높은 신뢰도의 예측을 할 것이다.
예측 신뢰는 다양한 방식으로 측정될 수 있고, 여기서 generalized entropy 개념을 사용한다.
- $G$ : $\Delta^{C}$에서 정의되는 미분 가능하고 concave 함수
- $p\in \Delta^{C}$, $p=(p_{1},\dots,p_{C})$, $p_{i}\ge0$ , $\sum_{i=1}^{C}p_{i}=1$
Bregman divergence : $D_{G}(p\Vert q)$, $p,q \in \Delta^{C}$
$$
D_{G}(\mathbf{p} \parallel \mathbf{q}):=G(\mathbf{q})-G(\mathbf{p})+(\mathbf{p}-\mathbf{q})^{\top}\nabla G(\mathbf{q})
$$
- q에서의 1차 테일러 전개와 $G(p)$값 간의 차이
- $G$ : concave
$G$는 $p$에 대해 permutation을 해도 변하지 않는다고 가정한다.
p와 u=1/C 사이의 Bregman divergence는 아래의 수식과 같이 negated generalized entropy로 축약된다.
$$
\begin{align}
D_G(\mathbf{p} \parallel \mathbf{u}) &= G(\mathbf{u}) - G(\mathbf{p}) + (\mathbf{p} - \mathbf{u})^{\top} \nabla G(\mathbf{u})\\
& \dot=-G(\mathbf{p})+\underbrace{(\mathbf{p}-\mathbf{u})^{\top}\nabla G(\mathbf{u})}_{=0}
\end{align}
$$
따라서 negated entropy를 점수로 사용하는 것은 predictive distribution $\mathbf{p}$와 uniform distribution $\mathbf{u}$의 통계적 거리로 해석될 수 있다. 특히 아래와 같은 수식에 주목한다.
$$G_{\gamma}(\mathbf{p})=\sum_{j}p_{j}^{\gamma}(1-p_{j})^{\gamma}$$
- $\gamma \in (0,1)$
- $p \mapsto p^{\gamma}(1-p)^{\gamma}$
$\gamma = \frac{1}{2}$
$$
G_{1/2}(\mathbf{p})=\sum_{j}\sqrt{p_{j}(1-p_{j})}
$$
이는 boosting 방법에서 발생하는 non-robust한 exponential loss와 연결되며 Shannon entropy($H(\mathbf{p})=-\sum_{j}p_{j}\log p_{j}$)보다 민감하게 작동한다.
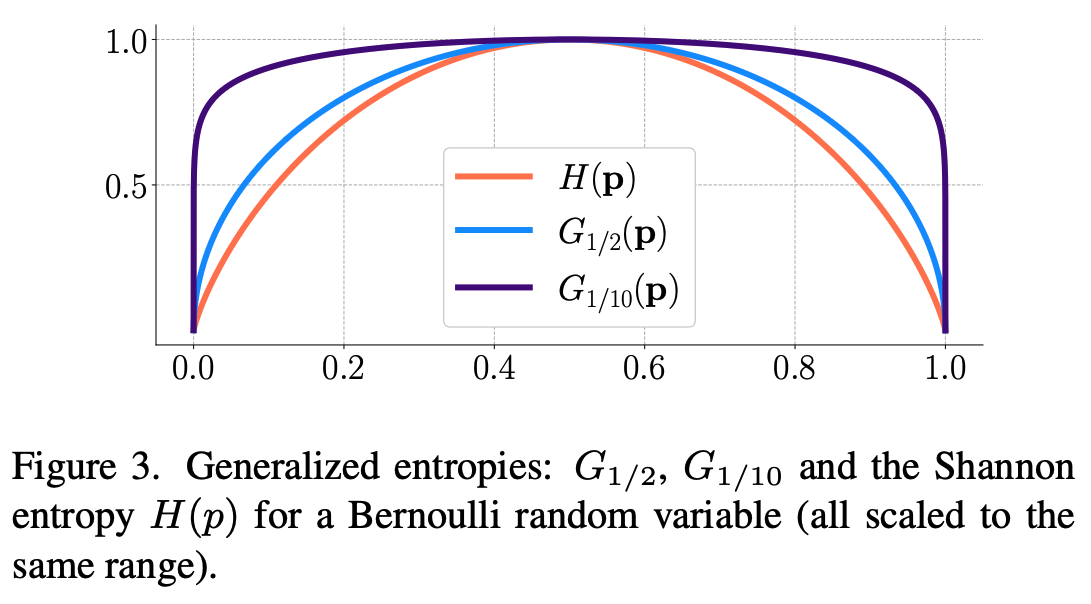
위 그림은 Bernoulli $p$에 대해 $H, G_{1/2}, G_{1/10}$의 그래프이다. $G_{1/10}$은 $p=0$과 $p=1$ 근처에서 빠르게 증가한다. 그러므로 $G_{1/10}$은 predictive distribution의 불확실성을 감지하는 매우 민감한 탐지기로 볼 수 있다.
요약하자면, Generalized Entropy(GEN)의 사용목적은 이상적인 one-hot에서 약간만 벗어나더라도 미세한 차이를 증폭시키는 것이다.
Truncation
예측 확률들을 내림차순 정렬한다면, $p_{j1} \ge p_{j2}\ge \cdots \ge p_{iC}$, $G_\gamma$는 매우 작은 확률 값들이 차지하는 큰 비중에 의해 지배될 수 있다. 작은 확률 값들의 미세한 변화가 점수에 영향을 미치게 된다. C가 증가할수록, 꼬리부분 때문에 $G_{\gamma}$의 순서가 바뀔 수 있다. 실험에서는 상위 $M$개의 class를 한정하여 합하는 방식이 더 강인하게 만들었다.
Experiments
본 논문의 실험에서는 ViM에서의 large-scale 평가 protocol을 수행했다.
ReAct* : ReAct의 local 버전의로 현재 sample의 activation값을 기준으로 clip하는 방식
특히, 평균 결과를 보게 되면 모든 post-hoc 방법과 비교할 때, GEN이 다양한 architecture에서 AUROC 점수가 높은 것을 알 수 있다. FPR95 측면에서도 다른 방법들보다 우수하다.
$M$과 $\gamma$에 대한 선택은 논문을 참고하면 알 수 있다. 실험적인 부분이라 제외하겠다.
Conclusion
- blackbox classifier에서 작동하는 간단하고 빠른 post-hoc OOD detection방법과 추가정보에 기반한 whitebox 방법간의 격차를 좁히는 것을 목표하였다.
- GEN은 구현이 간단하며 Classifier가 class확률을 제공하기만 하면 추가적인 조건이 필요하지 않다.
- GEN을 feature based method들과 결합하는 것도 방법이다.
- GEN이 최대 응답을 보이는 logit의 약 10%만 사용할때 최상의 성능을 발휘한다는 것을 발견했다.
- 이는 다른 방법들또한 마찬가지이다.
